Graphing Systems of Equations

Graphing systems of equations refers to solving systems of equations by graphing and tables. In algebra 2, this is one of the most important introductory lessons when it comes to learning about linear systems.

But if you’re a math teacher, you probably encountered at least one student that doesn’t find graphing systems of equations as the most fun lesson out there!

Luckily, there are various ways in which you can help students master this topic with great ease! Without further ado, here are some great guidelines that you can follow to help you best prepare for success in your classroom!

How to Teach Graphing Systems of Equations

What Is a System of Equations?

By now, students are familiar with what a linear equation is and what it looks like. You can start your lesson by asking them to provide a few examples of linear equations, or simply write a few linear equations on the whiteboard, such as:

y = 2x – 3
3x + 4y = 4
y + 3x – 1 = 0

Linear equations are equations that, when plotted on a graph, result in a straight line. The degree of x and y in a linear equation is always 1. You may also want to check out this article on teaching linear equations if students need further guidance in linear equations.

In this lesson, explain that you will be teaching about systems of linear equations. A system of linear equations is simply when we have a set of two (or more) linear equations that we need to work on together. Provide an example of systems of linear equations:

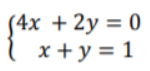
What Are Graphing Systems of Equations?

Explain that there are several ways in which we can solve systems of equations. This includes solving systems of equations by substitution, solving systems of equations by addition, etc. The easiest way is solving systems of equations by graphing.

We call this graphing systems of equations. So how do we perform this graphing of equations?

Ask students to think of linear equations again, for example, y = 2x – 3. The solution to this equation is an ordered pair (x, y) that worked in the equation.

For example, one solution to the equation y = 2x – 3 is the ordered pair (1, – 1) because by substituting the values for the variables in the equations, we see that they work and the equation is true.

Explain that when solving systems of equations by graphing, we need to find an ordered pair that is basically a solution to both of the linear equations in the given system of equations.

Point out that to do this, we need to plot the graph of each equation in the same coordinate system, which will result in two straight lines. Then we need to find the intersection of these two lines.

Highlight that the point of intersection, which is an ordered pair, represents the solution to the system of linear equations. The solution of systems of linear equations is correct if it satisfies the given equations. If the lines are parallel, there is no solution, as there isn’t any intersection.

Example:

Write an example of a system of equations on the whiteboard, for instance:

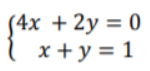
Point out that we’ll arrange each equation into the slope-intercept form. Remind students that the slope-intercept form is as follows: y = mx + b. M represents the slope, whereas b represents the y-intercept. You can also use this free video for more guidelines on the slope-intercept form.

So starting with the first equation, 4x + 2y = 0, if we rearrange it into the slope-intercept form, we’ll get y = – 2x. Then, we’ll pick some x values and then calculate the corresponding y values. For instance, if x = – 3, we can calculate that y = 6. Create a table for this purpose:

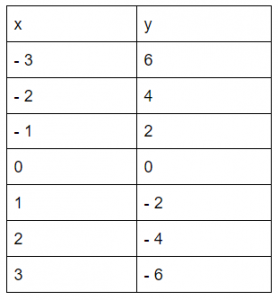
Now we’ll rearrange the second equation into the slope-intercept form. By doing this, x + y = 1 becomes y = 1 – x. Just like with the previous equation, we’ll pick some x values and then calculate the corresponding y values. Create a table for this purpose:

Point out that we can now plot the x, y points for both equations on the same coordinate plane. This will result in the following two lines:

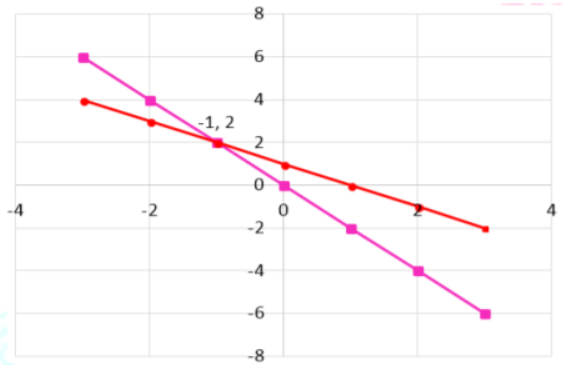
Remind students that the point of intersection for both lines is the solution for the system of equations. Since in this case, the lines intersect at (-1, 2), the solution is x = – 1 and y = 2. You can also verify the solution by substituting these values for the variables in the equations.

Additional Resources:

If you have the technical means in your classroom, you can also decide to use a video lesson to teach graphing systems of equations. Videos can provide added visual stimulation when teaching lessons that require drawing, such as graphing.

For example, you can use this free video that contains step-by-step instructions and worked-out examples of solving linear equations by graphing and gives you a way to check if the solution satisfies the given equations. This free video is another good resource.

Activities to Practice Graphing Systems of Equations

Pair Work

This simple activity will help students practice graphing systems of equations. The only thing you need to implement this activity in your classroom is this Assignment Worksheet (Members Only), which contains diverse exercises on graphing systems of equations.

Print out the above worksheet (one copy per student). Divide students into pairs and hand out the printouts. Provide instructions to students. Each student works individually to solve the exercises.

After some 15 minutes, they exchange their worksheets with the student in their pair and review the solutions. They’re supposed to provide critical feedback on each other’s work, which makes the activity great for peer tutoring as well.

Before You Leave…

If you enjoyed the math guidelines on graphing systems of equations that we shared in this article, you’ll want to check out our lesson that explains how to teach this topic in detail!

So if you’re looking for more math materials for children of all ages, join us in the Math Teacher Coach community or sign up for our emails to receive loads of free content!

Feel free to also check out our blog! You’ll find plenty of resources for all grades that will make teaching math a breeze!

This article is based on:

Unit 3 – Linear Systems