For students in algebra 2, linear equations are one of the most important lessons. Students learn how to create and solve linear equations in one variable, as well as linear equations in two variables. They also learn how to graph equations on coordinate axes with labels and scales.
All of this can be confusing for young learners, especially for students who may not be fully proficient with solving simpler one-variable equations from earlier grades. So it’s no surprise that some math teachers may also face difficulty when teaching this topic.
To help out, we’ve compiled a list of strategies that math teachers can adopt when teaching linear equations. Follow these math strategies and see your students’ knowledge soar!

What Are Linear Equations?
Linear equations are equations that, when plotted on a graph, result in a straight line. The degree of x and y in a linear equation is always 1.
Provide a few examples of equations so that students can learn to differentiate between linear and non-linear equations, such as:
- y = 8x – 9 (linear equation)
- y = x² – 7 (non-linear equation, because the x contains the exponent 2, hence it’s a second-degree equation)
- y + 3x – 1 = 0 (linear equation)
- y²- x = 9 (non-linear equation, because the y contains the exponent 2, hence it’s a second-degree equation)
- 3x – y = 1 (linear equation)
How to Teach Linear Equations
One-variable Linear Equations
When teaching linear equations, the first thing you’ll want to do is check kids’ knowledge of simpler one-variable equations and address any possible gaps. You can point out that linear equations in one variable are equations of the following form: ax + b = 0, where a and b are integers and x is a variable.
Now take any linear equation with one variable and provide step-by-step instructions on how to solve it, such as:
2x + 3 = -15
Remind students that the first thing that we want to do is get all the variables on one side of the equation and all the constant terms on the other side of the equation. Since the variable in the above example is already on the left, we’ll try to move 3 to the right hand of the equation.
Explain that we can achieve this by subtracting 3 from both sides of the equation. By doing so, the original 3 and the new 3 that we’re subtracting on the left side will cancel each other out and become 0.
In other words, we’ll have the following:
2x + 3 – 3 = -15 – 3
2x = – 18
To further simplify the equation, we’ll try to get rid of the constant 2 on the left. To do this, we’ll divide by 2 on both sides of the equation:
![]()
We can check the solution in the original solution:
2x + 3 = -15
By replacing – 9 for x, we’ll get:
2(-9) + 3 = -15
– 18 + 3 = – 15
– 15 = – 15
So the solution is correct!
You may also want to review kids’ knowledge on the properties of equality, as we apply these constantly when solving linear equations. You can check out our article that includes a bundle of freebies for more guidelines on the properties of equality.
Two-Variable Linear Equations
In algebra 2, linear equations with two variables are those equations that have two variables, the degree of which must be 1. Point out that linear equations with two variables have the following form: ax + by + c = 0
Also emphasize that while the solution to linear equations in one variable is a number, the solution to linear equations in two variables is an ordered pair. Provide an example of how to solve a linear equation with two variables, such as:
y = 2x – 3
Remind students that when we have an ordered pair, the first number is the x-coordinate and the second number is the y-coordinate, i.e. (x, y).
For instance, pick some x values that make it easy to calculate the corresponding y values. For instance, if x = 0, we can calculate that y = – 3:
y = 2x – 3
y = 2 (0) – 3
y = -3
Use this principle to find the other y values as well.
| x | y |
| 0 | – 3 |
| 1 | – 1 |
| 2 | 1 |
You can plot some of the x and y values that satisfy the equation and demonstrate to students that this equation will indeed produce a straight line on the graph! You can complement your lesson on linear equations with two variables with this free video.
Forms of Linear Equations
Point out to students that there are three main forms of linear equations, including:
- Slope-intercept form
- Point-slope form
- Standard form
Slope-intercept Form
Explain that we can recognize the slope-intercept form as y = mx + b. M represents the slope, whereas b represents the y-intercept. You can also use this free video for more guidelines on the slope-intercept form.
Point-slope Form
In the point-slope form, (y – y1) = m (x – x1), m represents the slope and (x1, y1) represent the coordinates of a point on the line. You can also use this free video for additional information on the point-slope form.
Standard Form
The standard form of a linear equation has the following form: ax + by = c, where a, b and c are integers and x and y are variables.

Rewriting Linear Equations
Once students are familiar with the different forms, you can move on to showing them how to rewrite linear equations from one form to another form. For instance, take a linear equation in standard form and rewrite it step by step in slope-intercept form:
3x + 4y = 4
Remind children that this equation is in standard form since it has the form of ax + by = c, where a, b and c are the integers 3, 4, and 4 again and x and y are the variables. We want to rewrite this linear equation into this form: y = mx + b.
To achieve this, we need to isolate the y on the left side. To that end, we’ll subtract 3x on both sides of the equation, to cancel out the 3x on the left:
3x + 4y = 4
3x – 3x + 4y = 4 – 3x
4y = 4 – 3x
Point out that since we’re left with 4y on the left and our aim is to have y all alone, we’ll divide by 4 on both sides of the equation:
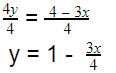
So there you have it! That’s our slope-intercept form. For additional guidelines on how to rewrite linear equations in all forms, you can also share this free video with your class.
Activities to Practice Linear Equations
Algebra 2: Linear Equations Game
This is an online game on advanced linear equations. This game will help children improve their skills in solving linear equations. Students should have a good knowledge of the properties of equality to be able to play the game. The only thing you’ll need is a sufficient number of devices.
Pair students up. Provide them with the instructions for the game. The goal is for each student to try to solve the linear equations on their device as quickly as possible. The game measures the number of correct answers, as well as the speed of solving an equation.
The first student that manages to work out all answers wins the game. If you’re a homeschooling parent, you can easily adjust this game to an individual game or simply have your older child join in!
Before You Leave…
If you enjoyed the math strategies that we shared in this article, you’ll want to check out our lessons that go in-depth in teaching linear equations!
If you’re looking for more math materials for children of all ages, join us in the Math Teacher Coach community or sign up for our emails to receive loads of free content! Feel free to also check out our blog! You’ll find plenty of resources for all grades that will make teaching math a breeze!


