Matrix Multiplication

Once algebra 2 students understand what a matrix represents, how to determine the order of a matrix, and how to organize data into matrices, they dive into matrix operations, including how to do matrix multiplication.

Even though lessons on matrix multiplication may seem overwhelming to students, rest assured that teaching multiplying matrices can be fun and easy, if you’re equipped with the right resources! So if you’re a math teacher looking for strategies to teach matrix multiplication, you’ve come to the right place!

These awesome teaching strategies on how to do matrix multiplication are guaranteed to keep your students engaged throughout the lesson!

Strategies to Teach Matrix Multiplication

What Is a Matrix?

By now, students probably already have an idea of what a matrix is. But it’s good to refresh their memory and this is a good opportunity to identify if there are gaps in some kids’ knowledge of matrices. So, start your lesson on matrix multiplication by defining matrices.

Explain that a matrix is a collection of information stored or arranged in an orderly fashion. A matrix represents an array of numbers. You can also remind students how to judge the order of any given matrix.

This is basically the number of rows × the number of columns in a given matrix. So if a matrix has n rows and m columns, its order will be n × m (point out that we read this as ‘n by m’). The number of rows and columns are the dimensions of a matrix.

It’s crucial that students understand how to determine the dimensions of a matrix, that is, how many rows and columns a matrix has, as this will be the starting point in their efforts to multiply matrices.

Write an example on the whiteboard of a matrix and ask students to determine its order:

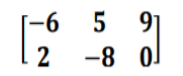
Students should be able to tell you that the matrix has two rows and three columns. This means that its order is 2 × 2, which we read two by two. Once students are comfortable in this area, move on to matrix multiplication.

How to Do Matrix Multiplication

Are Two Matrices Conformable for Multiplication?

The chief reason why students must be able to determine the number of rows and columns in a matrix in order to understand how to multiply matrices is because we can only multiply certain matrices, based on their number of rows and columns.

More specifically, two matrices A and B are conformable for multiplication AB if the number of columns in matrix A equals the number of rows in matrix B. You can also write on the whiteboard that we can multiply two matrices A and B only if:

Number of Columns in A = Number of Rows in B

You can write several examples on the whiteboard of two matrices that we’re trying to multiply. Ask students to determine which ones are conformable for multiplication, by applying the above-mentioned condition.

Can a 2 × 3 matrix be multiplied by a matrix that’s 3 × 3? Yes, because the number of columns in the first matrix is 3 and the number of rows in the second matrix is 3.
Can a 2 × 2 matrix be multiplied by a matrix that’s 2 × 2? Yes, because the number of columns in the first matrix is 2 and the number of rows in the second matrix is 2.
Can a 2 × 4 matrix be multiplied by a matrix that’s 1 × 2? No, because the number of columns in the first matrix is 4 and the number of rows in the second matrix is 1.

Step-by-Step Matrix Multiplication

Now you can show students how we carry out the process of multiplying two matrices that are conformable for multiplication. Let’s say there’s matrix A and matrix B that we wish to multiply. We can see that they’re 2 × 2, thus, conformable for multiplication.

In order to carry out the multiplication, we need to multiply the rows of the first matrix by the columns of the second matrix. A useful strategy is to circle the numbers in the rows and columns that you multiply in a different color.

You can also draw a visual representation in the following manner:

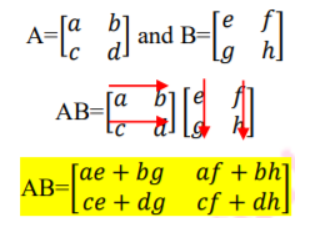
Example:

Let’s say we want to multiply the following two matrices:

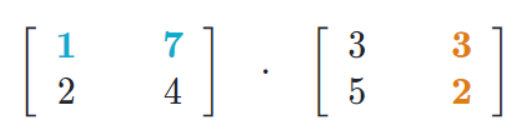
We start off by taking the product of the first row of the first matrix and the first column of the second matrix, that is, (1,7) and (3, 5). By applying the above rules, we’ll get:

1 × 3 + 7 × 5 = 3 + 35 = 38

This will represent the top left entry in our result. To get the top right entry, we’ll take the product of the first row of the first matrix and the second column of the second matrix, that is, (1, 7) and (3, 2). That is, we’ll take the products of the first terms and of the second terms and add them:

1 × 3 + 7 × 2 = 3 + 14 = 17

So 17 will be the top right entry. To find the bottom left entry, we need to take the product of the second row in the first matrix and the first column in the second matrix, that is (2, 4) and (3, 5):

2 × 3 + 4 × 5 = 6 + 20 = 26

So 26 will be the bottom left entry. To find the bottom-right entry, we need to take the product from the second row in the first matrix and the second column in the second matrix, that is (2, 4) and (3, 2):

2 × 3 + 4 × 2 = 6 + 8 = 14

With 14 as our bottom-right entry in the final result, we’ll get the following matrix:

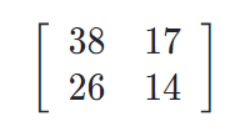
General Rules of Matrix Multiplication

Point out to students that there are a few general rules of matrix multiplication that are useful to know, including:

Multiplication is not commutative: A × B ≠ B × A
Associative Property applies: A × (B × C) = A × B × (C)
Multiplicative property of zero: A × 0 = 0
Multiplicative identity property: I × A = A × I = A
Distributive properties: A × (B + C) = A × B + B × C
(B + C) × A = B × A + C × A

Scalar Multiplication Vs. Matrix Multiplication

It’s advisable to draw the distinction between scalar multiplication and matrix multiplication. Explain that in scalar multiplication, we multiply one constant value with each element of a matrix, while in matrix multiplication, two conformable matrices are multiplied with each other.

Additional Resources:

Use this video by Khan Academy to demonstrate an example of multiplying a 2 × 2 matrix with a 2 × 2 matrix. Then, play this video to move on to a bit more complicated of a multiplication, where we have a multiplication of a 2 × 3 matrix and a 3 × 2 matrix.

This video is also a good resource on how to do matrix multiplication. The video contains simple guidelines on which matrices can be multiplied by which matrices, as well as practical examples on how to perform the process of multiplication.

Activities to Practice Matrix Multiplication

Matrix Spacecraft Game

This game will help students enhance their ability to determine whether two matrices are conformable for multiplication. To implement this activity in your classroom, you’ll need construction paper, some markers, and some drawing skills!

Draw two spacecraft on the construction paper, and write one matrix on one spacecraft and another matrix on the other. The matrices on the two spacecraft should be conformable for multiplication. Then, use the scissors to cut the spacecraft.

Create several of these ‘sets’ of spacecraft conformable for multiplication (10 sets per group, depending on the size of your class). Mix the spacecraft in different piles, making sure that there are corresponding matches in each pile so that you end up with 10 sets by matching them.

Divide students into small groups of 3 or 4. Hand out one pile of spacecraft to each group and provide instructions for the activity. The members of each group work together to determine which spacecraft can travel with which spacecraft in space.

To achieve this, students need to find the matrix on the inside of a given spacecraft that is conformable for multiplication with a matrix on the inside of another spacecraft. Once they find such two spacecraft, they match them. They proceed with this until all spacecraft are matched.

Give a few minutes to students, so they can match all spacecraft. Once the time is up, allow space for discussion. How did students determine whether a matrix was conformable for multiplication with another matrix? Did they have any unmatched matrices? What were the biggest challenges?

Multiply Two Matrices Game

This is an online game by IXL that will help students practice multiplying two matrices. To use this game in your classroom, the only thing you need is a sufficient number of technical devices (one per student), as well as a decent internet connection.

Divide students into pairs and provide instructions for the game. Explain to students that they are presented with several matrix multiplication exercises, where they have to complete the multiplication of the two given matrices, by filling in the missing number in the product.

Provide a few minutes for students to complete the exercises. You can also set a timer. In the end, students in each pair compare their final scores. The person with the highest score wins the game.

Multiply Matrices Game

In this online game by Khan Academy, students will have the opportunity to hone their skills at matrix multiplication. Make sure you have enough technical devices in your classroom (one per student) and start multiplying!

Students play the game individually, which makes it suitable for homeschooling parents as well. In each exercise, students are presented with two different matrices that they have to multiply. If they get stuck, they can also choose to watch a video or use a hint.

Provide a few minutes for students to finish the exercises. Then, open space for discussion and reflection. Were there any examples that they found particularly challenging? Which steps did they follow to fill in the entries in the final result?

Before You Leave…

If you like these teaching strategies and activities for how to do matrix multiplication, and you’re looking for more algebra 2 resources, make sure to sign up for our emails to receive loads of free lessons and content!

In addition, you can sign up for a membership on MathTeacherCoach or head over to our blog, where you’ll find more math materials for kids of all ages. You’ll discover that with the resources we offer, teaching math has never been easier!

This article is based on:

Unit 4 – Matrices